受検生の皆様、保護者の皆様、昨日2/3入試お疲れ様でした。
本年度の県立中等入試も無事に終わりホッと一息と言ったところでしょうか。
私の方も昨日楽しく適性検査の問題を解かせていただきました。

うちの生徒さんたちが
「どんな風に臨んだかな？」
「コレちゃんと樹形図書いたかな？」
「計算間違いしていないかな？」
と、個々の顔を思い浮かべながら解いておりました。

さて、今回の受検者数集計が出ましたのでまずはこちら。

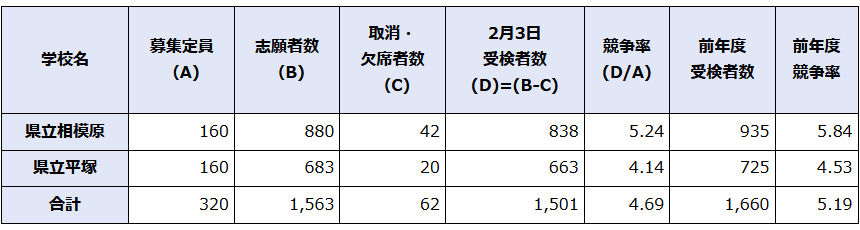
取消し、欠席を入れて平塚中等は最終倍率4.14倍。
辞退による繰り上げをほんの少し入れて最終的には実質4.0倍と言ったところでしょうか。

それでは本日「適性検査Ⅰ」について考察してまいります。

本年度からは問題難易度を、易level1～難level5として考えていこうと思います。
なるべく受検生目線で考えていきたいと思っています。

また、問5が新しく加わり(゜Д゜)

グル活が消滅した年に「グル活内容を作文で出す」と思っていたのですが、その年もその翌年も出なかったので「そーゆーのやらないんだ～」とたかをくくっていたら、、、まさかの本年来ちゃいました＠＠；

とはいえ、設問数的にはそこまで圧迫するような事態ではなかったので受検生にとってはあまり影響はなかったと考えています。

問1

(1)Level2

恒例の全て選べ系ですが、考えにくい割合計算や判断に迷うグレー系の選択肢もありません。

問1全体像として最初「何言ってんだこれ？」的な圧はありますが、設問自体は特に難しくありませんでした。如何に平常心で臨めたかどうか？にかかっていると思います。

(2)Level2

[装置の使い方]の説明文がやたら長く、こちらも文字数で圧をかけてきておりますが4番目の説明内に「10回動かしたときに52mちょうど」という記述があります。

1回動かして[装置]4個分、
2回動かして[装置]5個分
・・・
10回動かして[装置]13個分
4m×13個分＝52m

つまり125回動かす＝装置128個分と理解できれば
4m×128個分＝512mと出すことができます。

問2

(1)アLevel1

たろう君の発言に沿って計算するだけ。
最も高い～という指示より形の「最も長い長さ」を高さとし、その合計(あ)を4で割るだけ。

17×2+13+11×3+9×2+7+5×2+3×3=124
124÷4=31

(1)イLevel3

ここでようやく標準難易度登場ですね！

(1)アで間違えてしまうと(1)イは出来ないようになっています。
31cmとなる高さの組み合わせを考えていきます。
4人を便宜上A君、B君、C君、D君とすると
A(3／11／17)、B(3／11／17)、C(7／11／13)、D(3／5／5／9／9)
最も多い箱数はD君5箱となります。

(2)アLevel4

今回の適性検査Ⅰ内だけで言えばこの問2(2)と問4(2)が難問題と見ています。
Level5相当は「令和5年の問4レベル」にプレゼントしたいので今回は無しで＾＾；

(1)イに引き続き試行系問題。
高さの総合計を4で割り考えていくと時間的な余裕もなく、またこの出題形式ですとかえって難しくなります。選択肢を利用して逆算できたかどうかがポイントです。そこに気付ければ意外と早く片付ける事が出来た子もいると思います。

まずは①の12cmから検証。

A(3／3／3／3)、B(3／3／3／3)、C(3／3／3／3)、D(5／7)

あれ？出来てしまった・・・
で終了。

(2)イLevel4

これも(2)ア同様に選択肢から検証していきます。
※最も高くなるように～のため⑦から検証します。

⑦31cm

まず31cm×4人=124cm
これは各形の最大値の合計を超えてしまうので不適
※15×3+11×5+5×2+3×4=122

⑥30cm

A(15／15)、B(7／11／3／3／3／3)、C(8／8／8／3／3)、D(残りは8-3-11の箱1つのみ)
よって不適

⑤29cm

A(15／11／3)、B(15／11／3)、C(15／11／3)、D(8／8／5／5／3)
できた～♪でこちらが正答。

問3

(1)Level3

資料から計算を行い全て選ぶといういつもな感じの問題。
問1の全て選べ系で差がつきにくいので、こちらはぜひ取っておきたい問題です。
落ち着いて記述該当箇所を探し、落ち着いて割合計算できれば必ず取れますが、些細な見間違えや単位換算ミス、焦り等で間違えていたとしたら残念です。。。涙

(2)アLevel2

もうこの手の問題は公中検模試や各適性検査用のテキスト、過去問で散々練習しているはず。
きちんと復習を積み重ねてきた子であれば確実に取れていることでしょう。

30×0.21+35×0.15=11.55
11.55÷55×100=21%

(2)イLevel2

(2)ア同様。会話文に沿って一つ一つ丁寧にあ～うを埋めていくことが出来れば大丈夫。

あ：60÷0.15=400
い：2060×(300÷100)=6180
う：250×(400÷100)=1000

よって6180÷1000=6.18

問4

(1)アLevel1

[カードの取り方]を続けていけばOK

12345→23451→(2)3451→3451→4513→(4)513→513→135→(1)35→35→53→(5)3→3

(1)イLevel2

(1)アを利用してかなこさん、たろう君それぞれがどのカードを取ったか考えていくだけ。

会話文よりまず「わたし、たろうさんの順でひいた～」とあるので「かなこさん」→「たろうさん」の順でカードをゲットしていきます。

上の図より、かなこ(2)、たろう(4)、かなこ(1)、たろう(5)とカードを取っていることがわかります。

したがって今回「え」に入る数字はたろうさんの取ったカードは「い＝4」「う＝5」(順不同)となり、4+5=9と導き出せます。

(2)Level4

適性Ⅰ最後のこの問題は少し難しいかもしれません。受検生が苦手とする場合の数＆試行系だからということがその理由です。

まず図の左abcde右という箇所を利用し、どの位置のカードが何番目に引かれるかという規則を見つけ出します。(1)を利用してあげるのがよいでしょう。

a=3番目、b＝1番目、c＝残るカード、d＝2番目、e＝4番目
となることがわかります。

会話文より「かなこさんがeの位置に5のカードを置いた」とあり、また引き順が「たろう→かなこ→たろう→かなこ」とあるため、eの位置にある5のカードはかなこさんが引くことがわかります。

よってかなこさんのカードは「5」と「？」という状況になります。

ここからはかなこさんのカードが「5と1」「5と2」「5と3」「5と4」というそれぞれの場合について整理しながら考えていきます。

1.かなこさんが「5と1」の場合

たろうさんは「2／3／4」のうち2枚を引くことになります。
「2と3」「2と4」「3と4」についてそれぞれ得点を考えます。

・かなこ「5と1」たろう「2と3」のケース(残りカード4)
かなこ5+1=6点、たろう2+3=5点→条件加味→かなこ6点+4=10点、たろう5点→たろう敗北
・かなこ「5と1」たろう「2と4」のケース(残りカード3)
かなこ5+1=6点、たろう2+4=6点→条件加味→かなこ6点、たろう6点→引き分け
・かなこ「5と1」たろう「3と4」のケース(残りカード2)
かなこ5+1=6点、たろう3+4=7点→条件加味→かなこ6点＋2=8点、たろう7点→たろう敗北

2.かなこさんが「5と2」の場合

たろうさんは「1／3／4」のうち2枚を引くことになります。
「1と3」「1と4」「3と4」についてそれぞれ得点を考えます。

・かなこ「5と2」たろう「1と3」のケース(残りカード4)
かなこ5+2=7点、たろう1+3=4点→条件加味→かなこ7点、たろう4点＋4=8点→たろう勝利！
・かなこ「5と2」たろう「1と4」のケース(残りカード3)
かなこ5+2=7点、たろう1+4=5点→条件加味→かなこ7点+3＝10点、たろう5点＋3=8点→たろう敗北
・かなこ「5と2」たろう「3と4」のケース(残りカード1)
かなこ5+2=7点、たろう3+4=7点→条件加味→かなこ7点+1＝8点、たろう7点＋1=8点→引き分け

3.かなこさんが「5と3」の場合

たろうさんは「1／2／4」のうち2枚を引くことになります。
「1と2」「1と4」「2と4」についてそれぞれ得点を考えます。

・かなこ「5と3」たろう「1と2」のケース(残りカード4)
かなこ5+3=8点、たろう1+2=3点→条件加味→かなこ8点+4=12点、たろう3点→たろう敗北！
・かなこ「5と3」たろう「1と4」のケース(残りカード2)
かなこ5+3=8点、たろう1+4=5点→条件加味→かなこ8点+2=10点、たろう5点→たろう敗北！
・かなこ「5と3」たろう「2と4」のケース(残りカード1)
かなこ5+3=8点、たろう2+4=6点→条件加味→かなこ8点、たろう6点→たろう敗北！

4.かなこさんが「5と4」の場合

たろうさんは「1／2／3」のうち2枚を引くことになります。
「1と2」「1と3」「2と3」についてそれぞれ得点を考えます。

・かなこ「5と4」たろう「1と2」のケース(残りカード3)
かなこ5+4=9点、たろう1+2=3点→条件加味→かなこ9点+3=12点、たろう3点+3=6点→たろう敗北！
・かなこ「5と4」たろう「1と3」のケース(残りカード2)
かなこ5+4=9点、たろう1+3=4点→条件加味→かなこ9点、たろう4点+2=6点→たろう敗北！
・かなこ「5と4」たろう「2と3」のケース(残りカード1)
かなこ5+4=9点、たろう2+3=5点→条件加味→かなこ9点+1=10点、たろう5点+1=6点→たろう敗北！

と全て挙げてみましたがかなこさんが「5と4」の時点でたろうの敗北は濃厚です。
適性検査のトラップくぐりのために念のため次年度以降の受検生はきちんと検証するとよいでしょう。

ここでは太字下線の1パターンのみ、たろう君勝利となります。
ここで問われているのはa~dのあてはめ方となりますので、下記の2通りが正答となります。

(a,b,c,d)=(1,3,4,2)(3,1,4,2)

問5

Level3

最後の作文ですが、ある意味新傾向のためあまり言及いたしませんが、問に対して条件を満たし誤字や脱字、表現の間違え等がなければ点数をくれるものと見ています。
難易度も県立中等として標準的と思われます。

適性検査Ⅰについての予想ボーダー

今回の適性検査Ⅰはそこまでの難易度ではなかったと感じます。
まず目に入った問1でパニックにさえなっていなければ([装置の使い方]はホントいやらしく圧かけてますよね)非常に取り組みやすい検査だったと感じています。

予想平均は、今回のLevel1を9割で27点、Level2を7割取り84点、Level3を5割取り40点、Level4を2割取り14点とし165点といったところでしょうか。
もちろんこれより下がってくれるとありがたいのですが。。。汗

適性検査Ⅰだけで見る平塚中等ベースでの取っておいて欲しいボーダー点数は＋30～40点の195点～205点と見ています。
あくまで公中検模試の人数・偏差値分布から予測したものですので合否を保証するものではございません。

難易度自体は下がっているので昨年よりは合格ボーダーは上昇するとみています。
昨年は私自身、時間内に解ききれなかったり条件に気付けなかったりしましたが、今回は適性Ⅱで1問引っかかった(恥)以外スムーズに解くことが出来ました。

次回は適性検査Ⅱについて考察してみたいと思います。